Hartmann functions

Hello world

import tensorflow as tf
import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
import seaborn as sns

from scipy.optimize import minimize
from etudes.decorators import value_and_gradient, numpy_io

num_iterations = 50000
num_runs = 100

seed = 886  # set random seed for reproducibility
random_state = np.random.RandomState(seed)

alpha = np.array([1.0, 1.2, 3.0, 3.2])

A = {}
A[3] = np.array([[3.0, 10.0, 30.0],
                 [0.1, 10.0, 35.0],
                 [3.0, 10.0, 30.0],
                 [0.1, 10.0, 35.0]])
A[6] = np.array([[10.0,  3.0, 17.0,  3.5,  1.7,  8.0],
                 [0.05, 10.0, 17.0,  0.1,  8.0, 14.0],
                 [3.0,  3.5,  1.7, 10.0, 17.0,  8.0],
                 [17.0,  8.0,  0.05, 10.0,  0.1, 14.0]])
A[4] = A[6].T

P = {}
P[3] = 1e-4 * np.array([[3689, 1170, 2673],
                        [4699, 4387, 7470],
                        [1091, 8732, 5547],
                        [381,  5743, 8828]])
P[6] = 1e-4 * np.array([[1312, 1696, 5569,  124, 8283, 5886],
                        [2329, 4135, 8307, 3736, 1004, 9991],
                        [2348, 1451, 3522, 2883, 3047, 6650],
                        [4047, 8828, 8732, 5743, 1091,  381]])
P[4] = P[6].T

x_min = {}
x_min[3] = np.array([0.114614, 0.555649, 0.852547])
x_min[6] = np.array([0.20169, 0.150011, 0.476874, 0.275332, 0.311652, 0.6573])

axis = {}
axis[3] = -1
axis[6] = -1
axis[4] = -2

a = {}
a[3] = 0.0
a[4] = 1.1
a[6] = 0.0

b = {}
b[3] = 1.0
b[4] = 0.839
b[6] = 1.0

def make_hartmann_tf(alpha, A, P, a=0.0, b=1.0, axis=-1):

    @numpy_io
    @value_and_gradient
    def hartmann(x):

        r = tf.reduce_sum(A * tf.square(x - P), axis=axis)
        return (a - tf.reduce_sum(alpha * tf.exp(-r), axis=-1)) / b

    return hartmann

hartmann4d = make_hartmann_tf(alpha, A[4], P[4], a[4], b[4], axis[4])

Starting point

x_init = random_state.rand(4)
x_init

Out:

array([0.00140876, 0.75240707, 0.10057118, 0.4699249 ])

res = minimize(hartmann4d, x0=x_init, jac=True, method="L-BFGS-B", tol=1e-8)
res

Out:

     fun: -0.1182632861801847
hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>
     jac: array([-2.38112332e-07,  6.28465891e-07,  1.22074520e-05,  1.61916050e-06])
 message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
    nfev: 42
     nit: 27
  status: 0
 success: True
       x: array([0.40389835, 0.67337835, 0.35171053, 0.41247776])

x_min[4] = res.x

def make_hartmann(alpha, A, P, a=0.0, b=1.0, axis=-1):

    def hartmann(x):
        r = np.sum(A * np.square(x - P), axis=axis)
        return (a - np.dot(np.exp(-r), alpha)) / b

    return hartmann

frames = []

for dim in [3, 4, 6]:

    hartmann = make_hartmann(alpha, A[dim], P[dim], a[dim], b[dim], axis[dim])

    xs = random_state.rand(num_runs, num_iterations, 1, dim)
    ys = hartmann(xs)
    y_min = hartmann(x_min[dim])

    df = pd.DataFrame(np.minimum.accumulate(np.abs(y_min - ys), axis=1))
    df.index.name = "run"
    df.columns.name = "iteration"

    s = df.stack()
    s.name = "regret"

    frame = s.reset_index()
    frames.append(frame.assign(name=f"Hartmann {dim}D"))

data = pd.concat(frames, axis="index", sort=True)

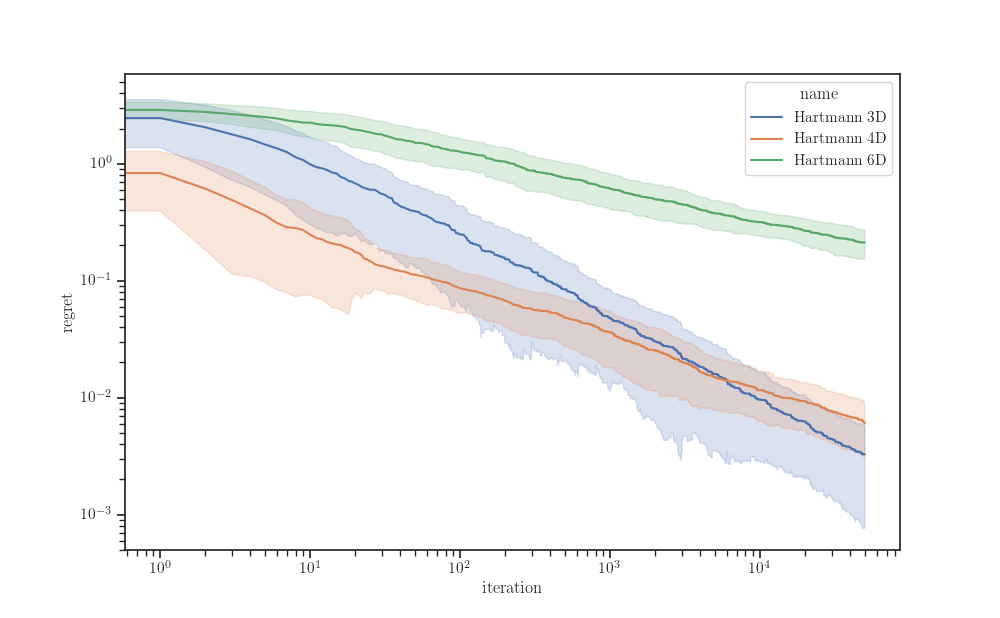
fig, ax = plt.subplots()

sns.lineplot(x="iteration", y="regret", hue="name",
             # units="run", estimator=None,
             ci="sd", palette="deep", data=data, ax=ax)
ax.set_xscale("log")
ax.set_yscale("log")

plt.show()