Note
Click here to download the full example code
GP Hyperparameter Estimation¶
We fit the hyperparameters of a Gaussian process by maximizing the marginal likelihood. This is commonly referred to as empirical Bayes, or type-II maximum likelihood estimation.
import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import seaborn as sns
import pandas as pd
from collections import defaultdict
from etudes.datasets.synthetic import (synthetic_sinusoidal,
make_regression_dataset)
# shortcuts
tfd = tfp.distributions
kernels = tfp.math.psd_kernels
def to_numpy(transformed_variable):
return tf.convert_to_tensor(transformed_variable).numpy()
# constants
num_train = 25 # nbr training points in synthetic dataset
num_features = 1 # dimensionality
num_index_points = 256 # nbr of index points
num_samples = 8
num_epochs = 100
learning_rate = 0.05
beta_1 = 0.5
beta_2 = 0.99
observation_noise_variance_true = 1e-1
jitter = 1e-6
kernel_cls = kernels.ExponentiatedQuadratic
seed = 42 # set random seed for reproducibility
random_state = np.random.RandomState(seed)
x_min, x_max = -1.0, 1.0
X_grid = np.linspace(x_min, x_max, num_index_points).reshape(-1, num_features)
load_data = make_regression_dataset(synthetic_sinusoidal)
X, Y = load_data(num_train, num_features,
observation_noise_variance_true,
x_min=x_min + 0.5, x_max=x_max - 0.5,
random_state=random_state)
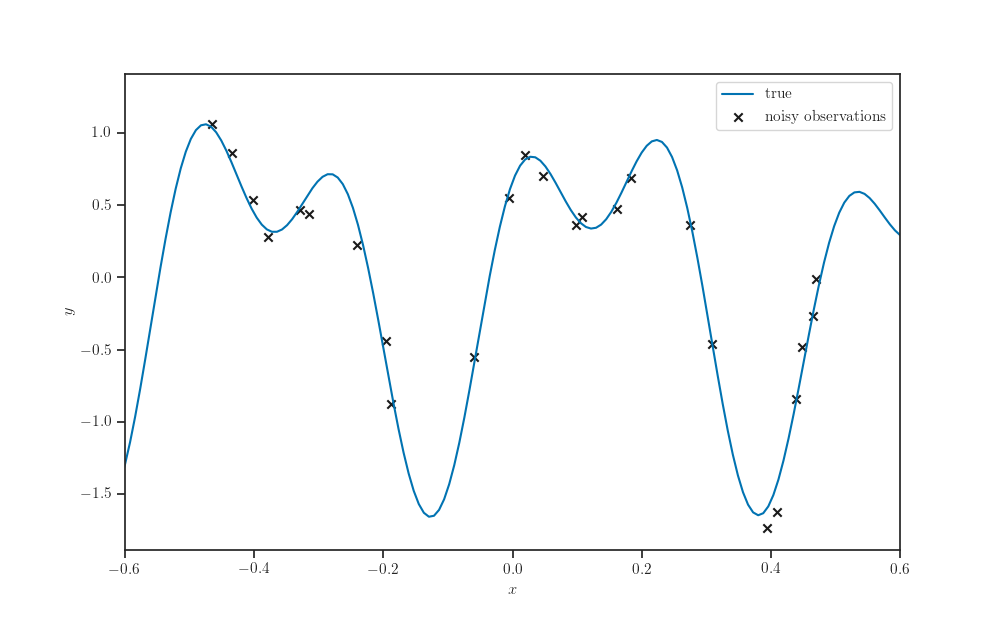
Synthetic dataset¶
fig, ax = plt.subplots()
ax.plot(X_grid, synthetic_sinusoidal(X_grid), label="true")
ax.scatter(X, Y, marker='x', color='k',
label="noisy observations")
ax.legend()
ax.set_xlim(x_min + 0.4, x_max - 0.4)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
plt.show()
Define and initialize the kernel parameters and model observation noise variables.
amplitude = tfp.util.TransformedVariable(
1.0, bijector=tfp.bijectors.Exp(), dtype="float64", name='amplitude')
length_scale = tfp.util.TransformedVariable(
0.5, bijector=tfp.bijectors.Exp(), dtype="float64", name='length_scale')
observation_noise_variance = tfp.util.TransformedVariable(
1e-1, bijector=tfp.bijectors.Exp(), dtype="float64",
name='observation_noise_variance')
Define Gaussian Process model
kernel = kernel_cls(amplitude=amplitude, length_scale=length_scale)
gp = tfd.GaussianProcess(
kernel=kernel, index_points=X,
observation_noise_variance=observation_noise_variance)
Gradient-based optimizer
optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate,
beta_1=beta_1,
beta_2=beta_2)
Training loop
history = defaultdict(list)
for epoch in range(num_epochs):
with tf.GradientTape() as tape:
nll = - gp.log_prob(Y)
gradients = tape.gradient(nll, gp.trainable_variables)
optimizer.apply_gradients(zip(gradients, gp.trainable_variables))
history["nll"].append(to_numpy(nll))
history["amplitude"].append(to_numpy(amplitude))
history["length_scale"].append(to_numpy(length_scale))
history["observation_noise_variance"].append(to_numpy(observation_noise_variance))
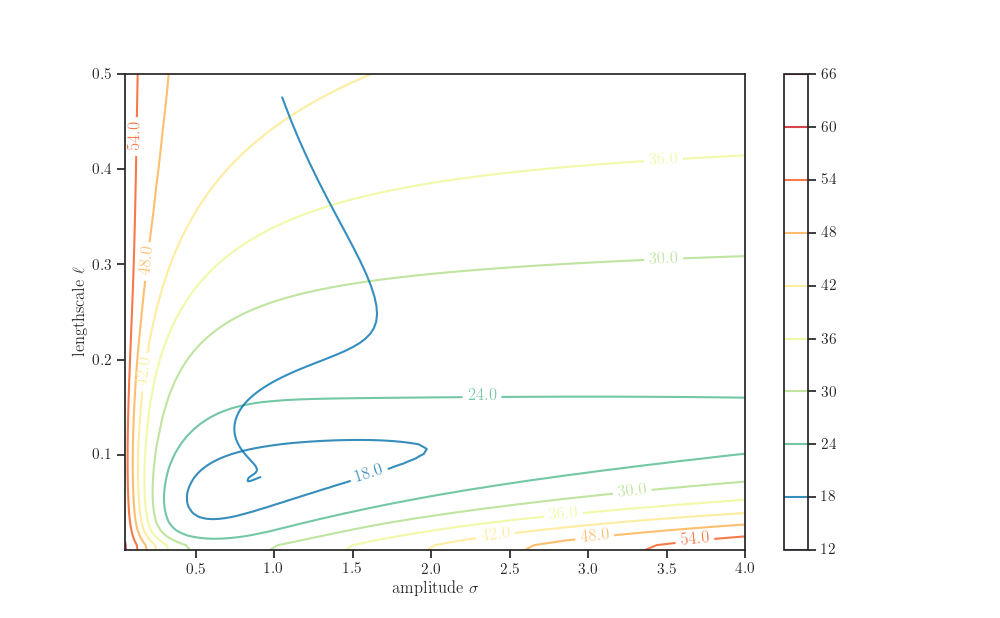
amplitude_grid, length_scale_grid = np.ogrid[5e-2:4.0:100j, 1e-5:5e-1:100j]
kernel_grid = kernel_cls(amplitude=amplitude_grid,
length_scale=length_scale_grid)
gp_grid = tfd.GaussianProcess(
kernel=kernel_grid,
index_points=X,
observation_noise_variance=observation_noise_variance_true)
nll_grid = - gp_grid.log_prob(Y)
fig, ax = plt.subplots()
contours = ax.contour(*np.broadcast_arrays(amplitude_grid, length_scale_grid),
nll_grid, cmap="Spectral_r")
sns.lineplot(x='amplitude', y='length_scale',
sort=False, data=pd.DataFrame(history), alpha=0.8, ax=ax)
fig.colorbar(contours, ax=ax)
ax.clabel(contours, fmt='%.1f')
ax.set_xlabel(r"amplitude $\sigma$")
ax.set_ylabel(r"lengthscale $\ell$")
plt.show()
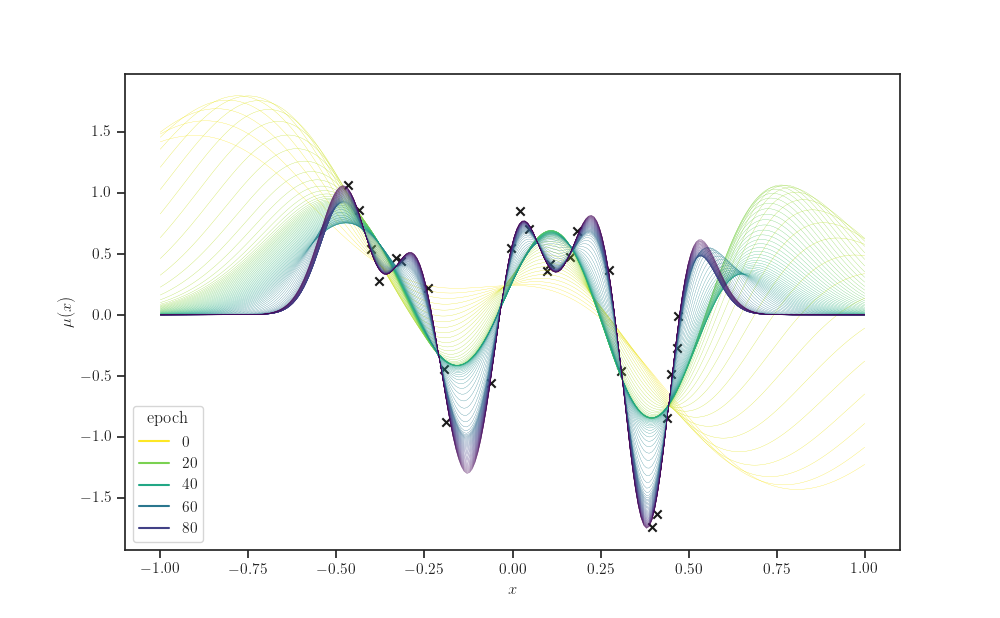
kernel_history = kernel_cls(amplitude=history["amplitude"],
length_scale=history["length_scale"])
gprm_history = tfd.GaussianProcessRegressionModel(
kernel=kernel_history, index_points=X_grid,
observation_index_points=X, observations=Y,
observation_noise_variance=history["observation_noise_variance"],
jitter=jitter)
gprm_mean = gprm_history.mean()
gprm_stddev = gprm_history.stddev()
# "Melt" the dataframe
d = pd.DataFrame(gprm_mean.numpy(), columns=X_grid.squeeze())
d.index.name = "epoch"
d.columns.name = "x"
s = d.stack()
s.name = "y"
data = s.reset_index()
data
fig, ax = plt.subplots()
sns.lineplot(x='x', y='y', hue="epoch", palette="viridis_r", data=data,
linewidth=0.2, ax=ax)
ax.scatter(X, Y, marker='x', color='k', label="noisy observations")
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$\mu(x)$')
plt.show()
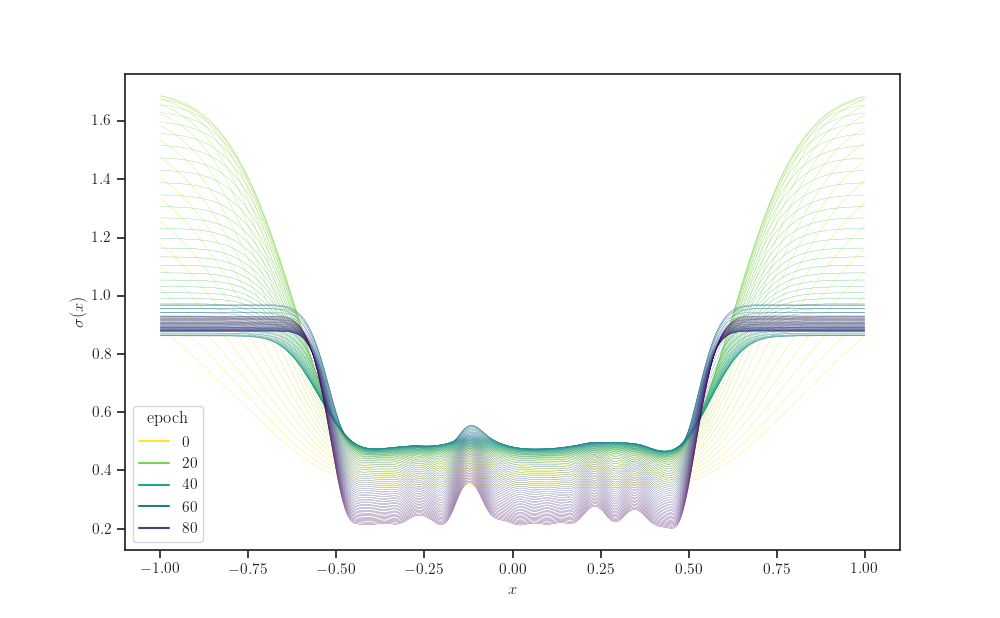
# "Melt" the dataframe
d = pd.DataFrame(gprm_stddev.numpy(), columns=X_grid.squeeze())
d.index.name = "epoch"
d.columns.name = "x"
s = d.stack()
s.name = "y"
data = s.reset_index()
data
fig, ax = plt.subplots()
sns.lineplot(x='x', y='y', hue="epoch", palette="viridis_r", data=data,
linewidth=0.2, ax=ax)
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$\sigma(x)$')
plt.show()
Animation
fig, ax = plt.subplots()
line_mean, = ax.plot(X_grid, gprm_mean[0], c="steelblue")
line_stddev_lower, = ax.plot(X_grid, gprm_mean[0] - gprm_stddev[0],
c="steelblue", alpha=0.4)
line_stddev_upper, = ax.plot(X_grid, gprm_mean[0] + gprm_stddev[0],
c="steelblue", alpha=0.4)
ax.scatter(X, Y, marker='x', color='k', label="noisy observations")
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
def animate(i):
line_mean.set_data(X_grid, gprm_mean[i])
line_stddev_lower.set_data(X_grid, gprm_mean[i] - gprm_stddev[i])
line_stddev_upper.set_data(X_grid, gprm_mean[i] + gprm_stddev[i])
return line_mean, line_stddev_lower, line_stddev_upper
anim = animation.FuncAnimation(fig, animate, frames=num_epochs,
interval=60, repeat_delay=5, blit=True)
Total running time of the script: ( 0 minutes 30.080 seconds)