Gaussian Process Regression with Automatic Relevance Determination (ARD)

Hello world

import numpy as np

import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()

import tensorflow_probability as tfp

import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

from sklearn.datasets import load_boston
from sklearn.preprocessing import normalize
from sklearn.utils import shuffle

from collections import defaultdict

# shortcuts
tfd = tfp.distributions
kernels = tfp.math.psd_kernels

# environment
golden_ratio = 0.5 * (1 + np.sqrt(5))


def golden_size(width):
    return (width, width / golden_ratio)


width = 10.0

rc = {
    "figure.figsize": golden_size(width),
    "font.serif": ['Times New Roman'],
    "text.usetex": False,
}

sns.set(context="notebook",
        style="ticks",
        palette="colorblind",
        font="serif",
        rc=rc)

# constants
boston = load_boston()

num_train, num_features = boston.data.shape
num_epochs = 500

kernel_cls = kernels.MaternFiveHalves

jitter = 1e-6
seed = 42  # set random seed for reproducibility
random_state = np.random.RandomState(seed)

The dataset has 506 datapoints, with 13 continuous/categorical features and a single target, the median property value.

X, Y = shuffle(normalize(boston.data),
               boston.target,
               random_state=random_state)

print(X.shape, Y.shape)

Out:

(506, 13) (506,)

We can load this dataset into a Pandas DataFrame for ease of visualization.

boston_df = pd.DataFrame(boston.data, columns=boston.feature_names) \
              .assign(MEDV=boston.target)

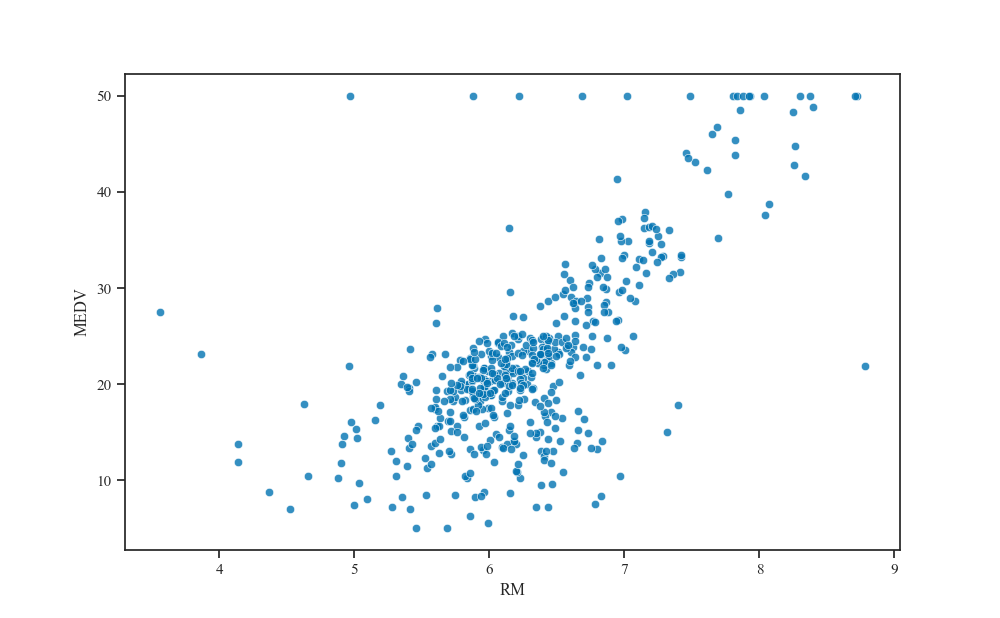
For example, we can see how the median property value (MEDV) varies with the average number of rooms per dwelling (RM).

fig, ax = plt.subplots()

sns.scatterplot(x="RM", y="MEDV", data=boston_df, alpha=.8, ax=ax)

plt.show()

Empirical Bayes (maximizing the log marginal likelihood)

Now let us fit a GP regression model to this dataset. We consider the Matern5/2 covariance function as before, except now, we use the anisotropic variant of the kernel. That is, we incorporate a lengthscale vector of 13 positive scalar values.

These hyperparameter values determine how far you need to move along a particular axis in the input space for the function values to become uncorrelated. By estimating these values we effectively implement automatic relevance determination, as the inverse of the lengthscale determines the relevance of the dimension. If the lengthscale is very large, the covariance will practically become independence of that input, and effectively remove it from the inference (GPML Section 5.1 Rasmussen & Williams, 2006).

# Base (isotropic) kernel with some scalar base lengthscale
amplitude = tf.exp(tf.Variable(np.float64(0), name='amplitude'))
length_scale = tf.exp(tf.Variable(np.float64(-1), name='length_scale'))
base_kernel = kernel_cls(amplitude=amplitude, length_scale=length_scale)

# ARD (anisotropic) kernel with a vector of varying _effective_ lengthscales
scale_diag = tf.exp(tf.Variable(np.zeros(num_features), name='scale_diag'))
kernel = kernels.FeatureScaled(base_kernel, scale_diag=scale_diag)

# Finalize the model
observation_noise_variance = tf.exp(
    tf.Variable(np.float64(-5)),
    name='observation_noise_variance')

gp = tfd.GaussianProcess(
    kernel=kernel,
    index_points=X,
    observation_noise_variance=observation_noise_variance
)

# log marginal likelihood
nll = - gp.log_prob(Y)
nll

optimizer = tf.train.AdamOptimizer(learning_rate=0.05, beta1=0.5, beta2=.99)
optimize = optimizer.minimize(nll)

Training loop

history = defaultdict(list)

with tf.Session() as sess:

    sess.run(tf.global_variables_initializer())

    for i in range(num_epochs):
        (_, nll_value, amplitude_value, length_scale_value,
         observation_noise_variance_value, scale_diag_value) = sess.run([optimize, nll, amplitude, length_scale, observation_noise_variance, scale_diag])
        history["nll"].append(nll_value)
        history["amplitude"].append(amplitude_value)
        history["length_scale"].append(length_scale_value)
        history["observation_noise_variance"].append(observation_noise_variance_value)
        history["scale_diag"].append(scale_diag_value)

history_df = pd.DataFrame(history)

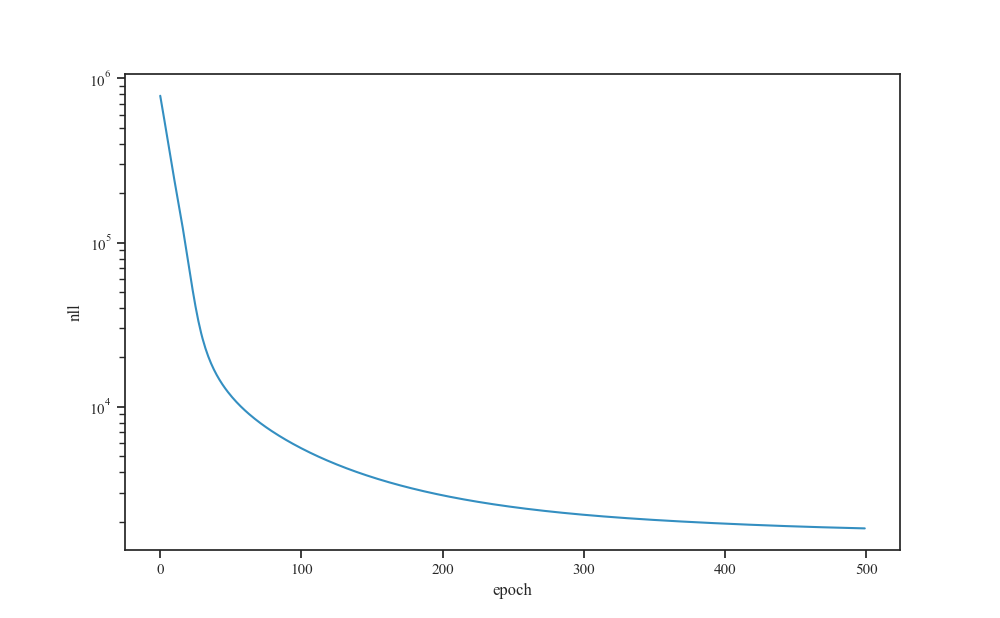
Learning curve

fig, ax = plt.subplots()

sns.lineplot(x='index', y='nll', data=history_df.reset_index(),
             alpha=0.8, ax=ax)

ax.set_xlabel("epoch")
ax.set_yscale("log")

plt.show()

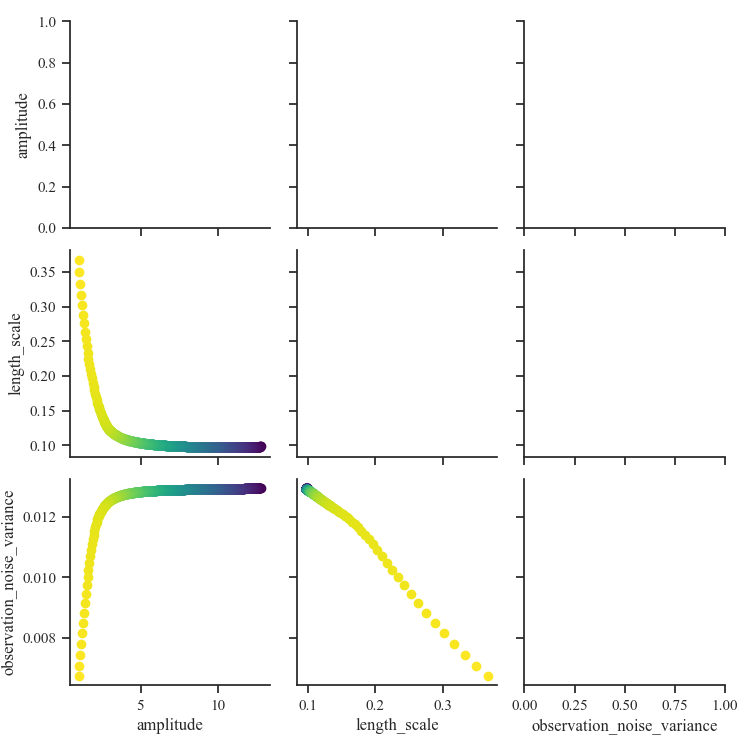
Visualize scalar hyperparameters over epochs

scalars = ["nll", "amplitude", "length_scale", "observation_noise_variance"]
scalars_history_df = history_df[scalars]

g = sns.PairGrid(history_df[scalars], hue="nll", palette="viridis")
g = g.map_lower(plt.scatter)

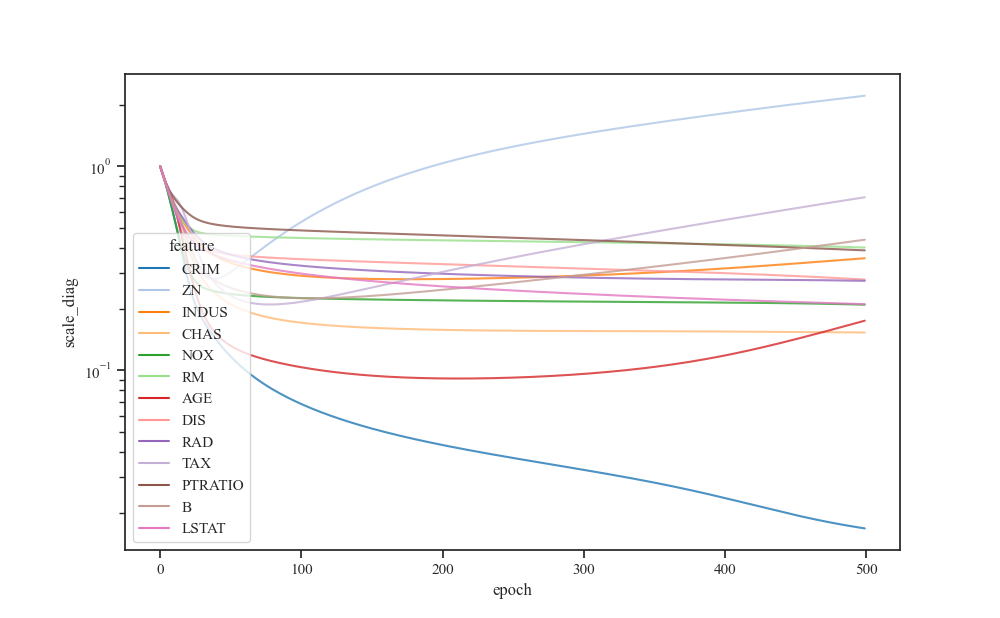
Visualize input feature scales over epochs

d = pd.DataFrame(history["scale_diag"], columns=boston.feature_names)
d.index.name = "epoch"
d.columns.name = "feature"
s = d.stack()
s.name = "scale_diag"
data = s.reset_index()

fig, ax = plt.subplots()

sns.lineplot(x='epoch', y="scale_diag", hue="feature", palette="tab20",
             sort=False, data=data, alpha=0.8, ax=ax)
ax.set_yscale("log")

plt.show()

Visualize Effective Lengthscales

We display the bar chart of the effective lengthscales corresponding to each dimension.

base_length_scale_final = scalars_history_df.length_scale.iloc[-1]

scale_diag_final = d.iloc[-1]
effective_length_scale_final = base_length_scale_final * scale_diag_final
effective_length_scale_final.name = "effective_length_scale"
data = effective_length_scale_final.reset_index()

fig, ax = plt.subplots()

sns.barplot(x='feature', y="effective_length_scale", palette="tab20",
            data=data, alpha=0.8, ax=ax)

plt.show()

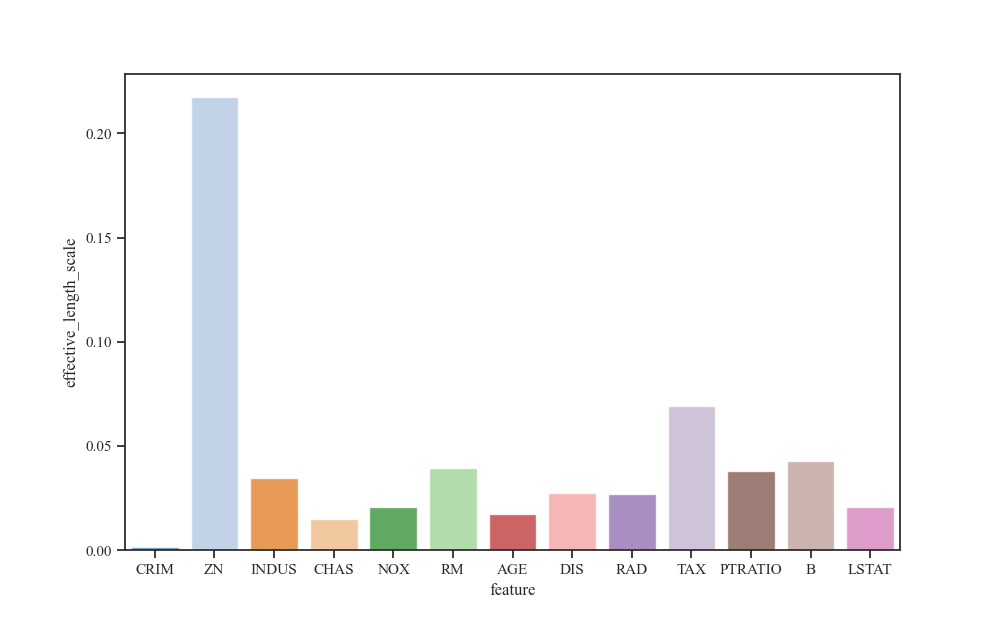
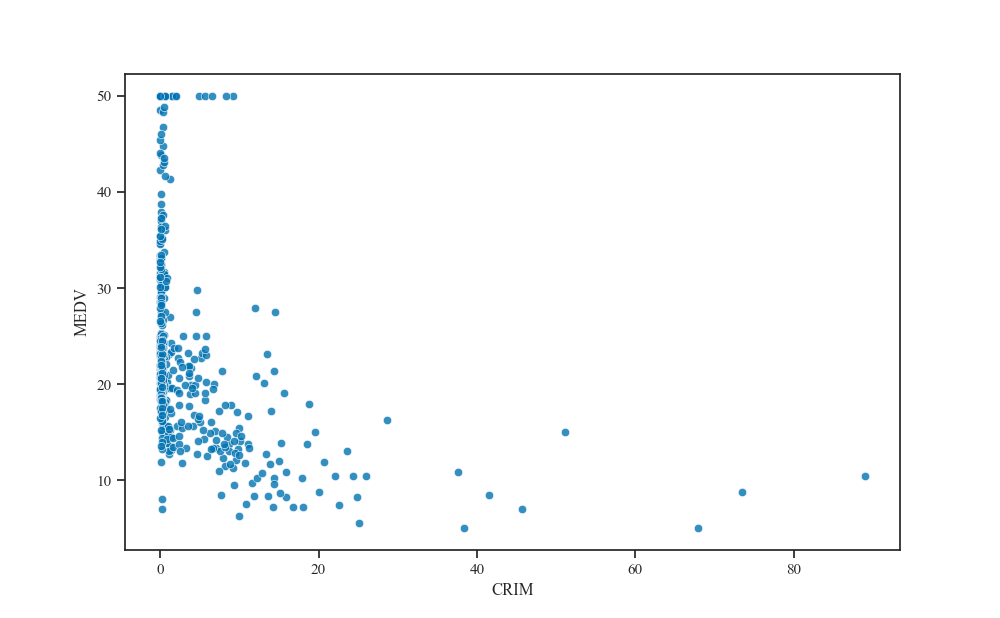
Generating the scatter plot with respect to the feature that has the smallest effective lengthscale, we find that it is indeed highly correlated with the median property value.

fig, ax = plt.subplots()

sns.scatterplot(x=effective_length_scale_final.idxmin(), y='MEDV',
                data=boston_df, alpha=.8, ax=ax)

plt.show()

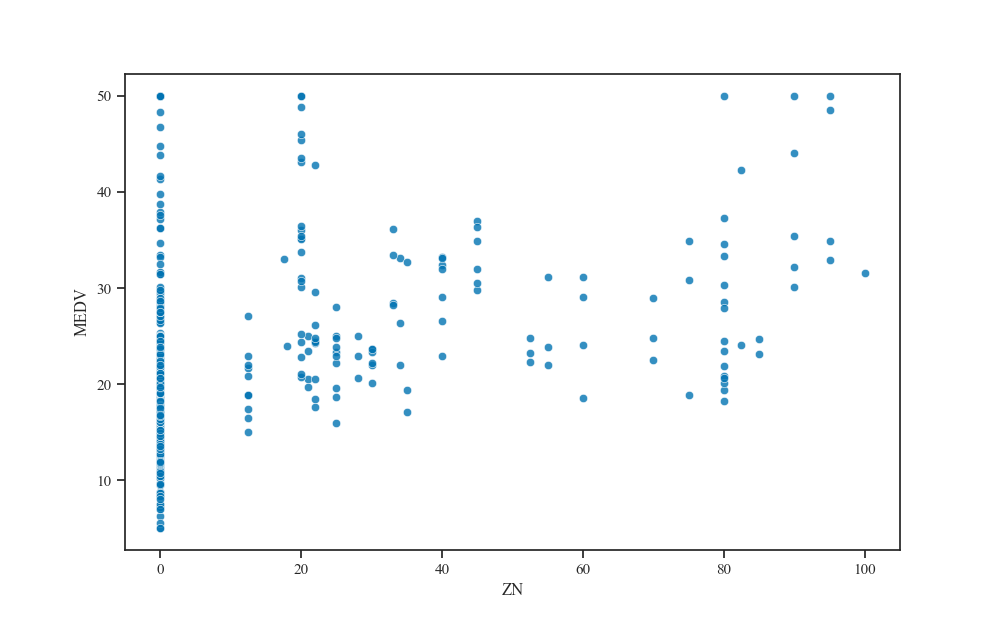
And vice versa for the feature with the largest effective lengthscale.

fig, ax = plt.subplots()

sns.scatterplot(x=effective_length_scale_final.idxmax(), y='MEDV',
                data=boston_df, alpha=.8, ax=ax)

plt.show()