Gaussian Process Posterior Predictive

Hello world

import numpy as np

import tensorflow_probability as tfp

import matplotlib.pyplot as plt

from etudes.datasets.synthetic import synthetic_sinusoidal, make_regression_dataset
from etudes.plotting import fill_between_stddev

# shortcuts
tfd = tfp.distributions
kernels = tfp.math.psd_kernels

# constants
num_train = 25  # nbr training points in synthetic dataset
num_features = 1  # dimensionality
num_index_points = 256  # nbr of index points
num_samples = 7

amplitude = 1.0
length_scale = 0.1

observation_noise_variance = 1e-1
jitter = 1e-6

kernel_cls = kernels.ExponentiatedQuadratic

seed = 42  # set random seed for reproducibility
random_state = np.random.RandomState(seed)

x_min, x_max = -1.0, 1.0
X_test = np.linspace(x_min, x_max, num_index_points).reshape(-1, num_features)

load_data = make_regression_dataset(synthetic_sinusoidal)
X_train, Y_train = load_data(num_train, num_features,
                             observation_noise_variance,
                             x_min=-0.5, x_max=0.5,
                             random_state=random_state)

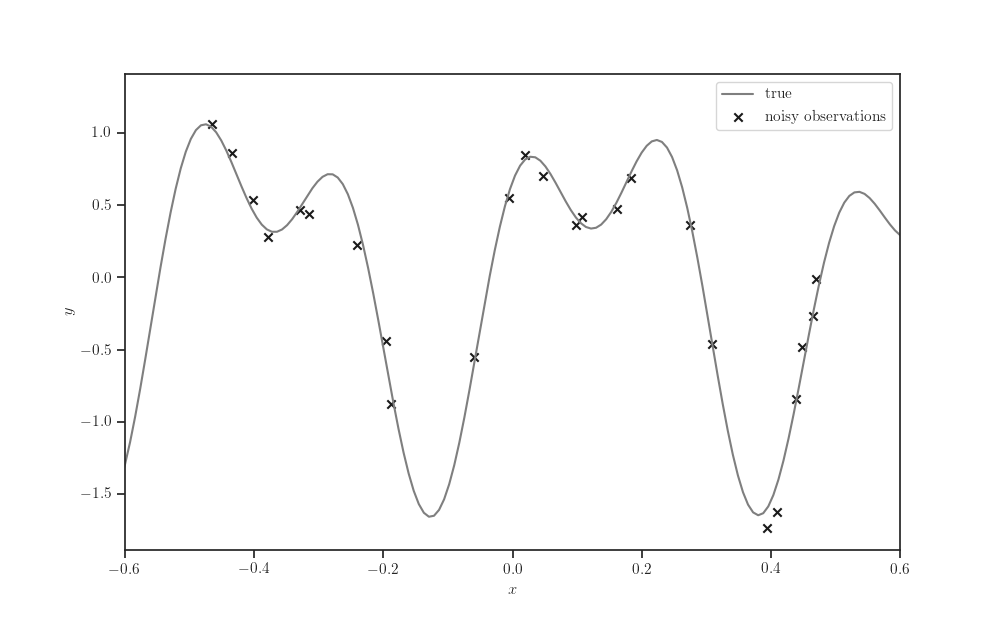
Synthetic dataset

fig, ax = plt.subplots()

ax.plot(X_test, synthetic_sinusoidal(X_test), label="true", color="tab:gray")
ax.scatter(X_train, Y_train, marker='x', color='k',
           label="noisy observations")

ax.legend()

ax.set_xlim(-0.6, 0.6)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')

plt.show()

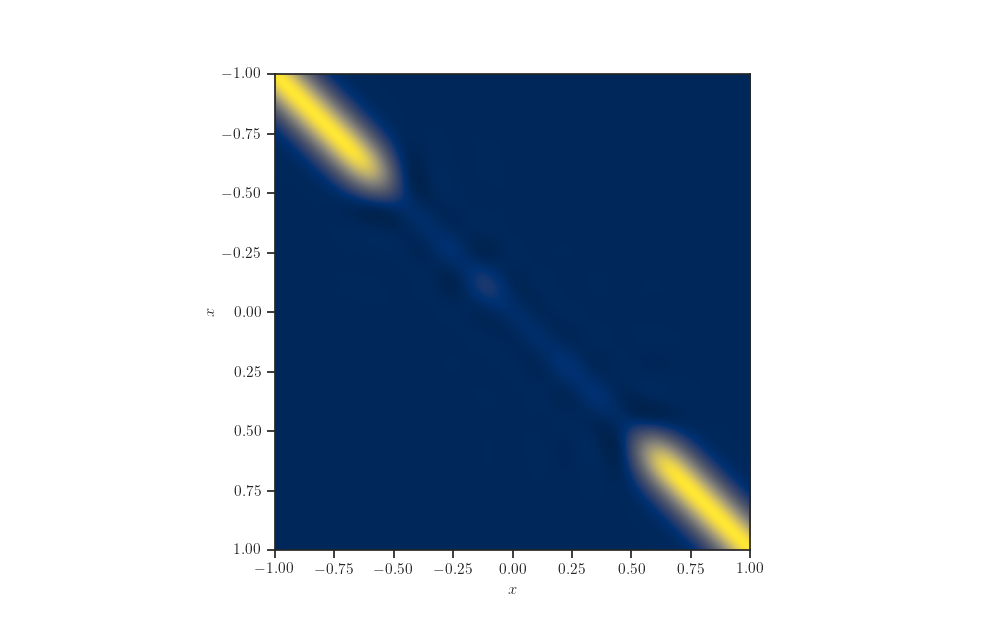
Schur Complement kernel matrix

kernel = kernel_cls(amplitude=np.float64(amplitude),
                    length_scale=np.float64(length_scale))
schur_complement_kernel = kernels.SchurComplement(
    kernel, X_train, diag_shift=observation_noise_variance)

fig, ax = plt.subplots()

ax.imshow(schur_complement_kernel.matrix(X_test, X_test),
          extent=[x_min, x_max, x_max, x_min], cmap="cividis")

ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$x$')

plt.show()

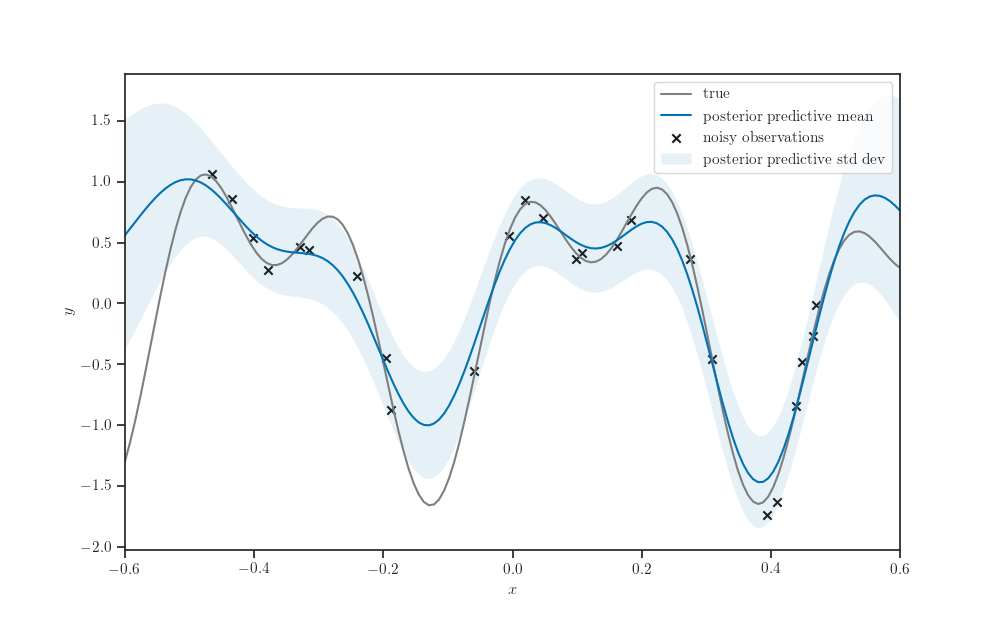
Posterior predictive distribution

gprm = tfd.GaussianProcessRegressionModel(
    kernel=kernel, index_points=X_test,
    observation_index_points=X_train,
    observations=Y_train,
    observation_noise_variance=observation_noise_variance,
    jitter=jitter
)

fig, ax = plt.subplots()

ax.plot(X_test, synthetic_sinusoidal(X_test), label="true", color="tab:gray")
ax.scatter(X_train, Y_train, marker='x', color='k',
           label="noisy observations")

ax.plot(X_test, gprm.mean(), label="posterior predictive mean")

fill_between_stddev(X_test.squeeze(),
                    gprm.mean().numpy().squeeze(),
                    gprm.stddev().numpy().squeeze(), alpha=0.1,
                    label="posterior predictive std dev", ax=ax)

ax.legend()

ax.set_xlim(-0.6, 0.6)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')

plt.show()

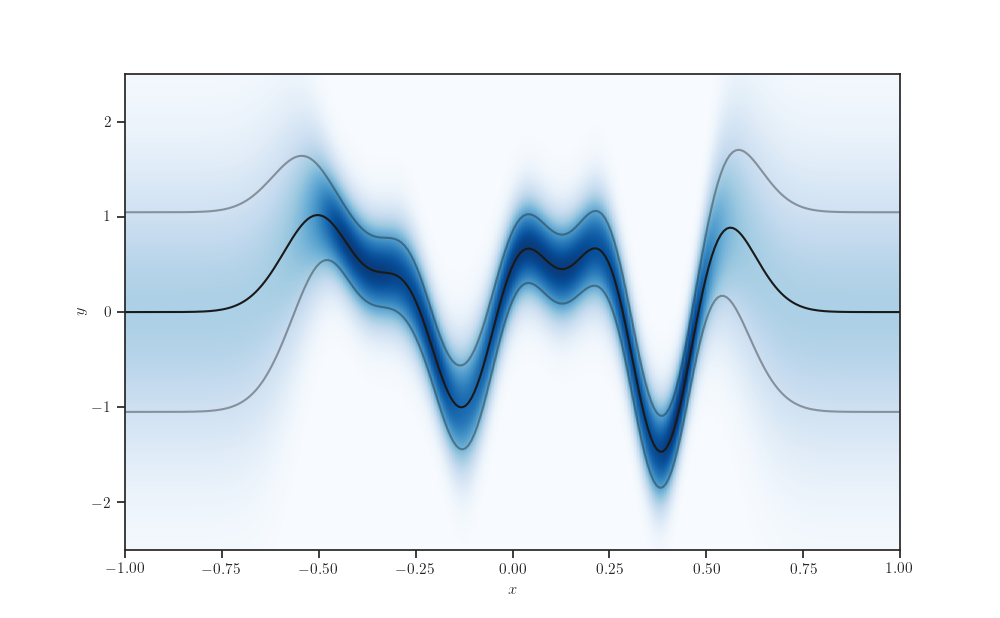
y_min, y_max = -2.5, 2.5
y_num_points = 512
gprm_marginals = tfd.Normal(loc=gprm.mean(), scale=gprm.stddev())
Y_q = np.linspace(y_min, y_max, y_num_points).reshape(-1, 1)

fig, ax = plt.subplots()

ax.imshow(gprm_marginals.prob(Y_q), origin="lower",
          extent=[x_min, x_max, y_min, y_max],
          aspect="auto", cmap="Blues")
ax.plot(X_test, gprm.mean(), color='k')

ax.plot(X_test, gprm.mean() - gprm.stddev(), color='k', alpha=0.4)
ax.plot(X_test, gprm.mean() + gprm.stddev(), color='k', alpha=0.4)

ax.set_xlabel('$x$')
ax.set_ylabel('$y$')

plt.show()